nl = 2d sinJ, n = integer.
Equipment used:
1) Scintag XDS 2000 X-ray powder diffractometer
2) TELTRON electron diffraction tube, TEL 555.
Objectives:
A) Demonstrate that X-rays and electrons both undergo diffraction and so both are wave-like.
B) Introduce some basic ideas in the description of structure of crystalline solids.
Various images that will be instructive for this lab are found here.
The Bragg Condition
Waves scatter and undergo diffraction when they strike a set of regularly spaced obstacles whose dimensions are of the order of the wavelength. A familiar optical example is the diffraction grating. Also the regularly spaced atoms in crystalline material are effective in scattering waves having wavelength comparable to atomic dimensions. X-rays are such waves, and X-ray diffraction has become a powerful tool for studying the arrangement of atoms in a crystal. But electrons, too, undergo diffraction from a crystal. We’re forced to conclude that electrons can act like waves with wavelength comparable to atomic dimensions! We are going to do what amounts to the same experiment with two different kinds of waves, X-rays and electrons. We’ll scatter these waves off powdered crystalline materials and find that the two cases give the same kind of diffraction pattern.
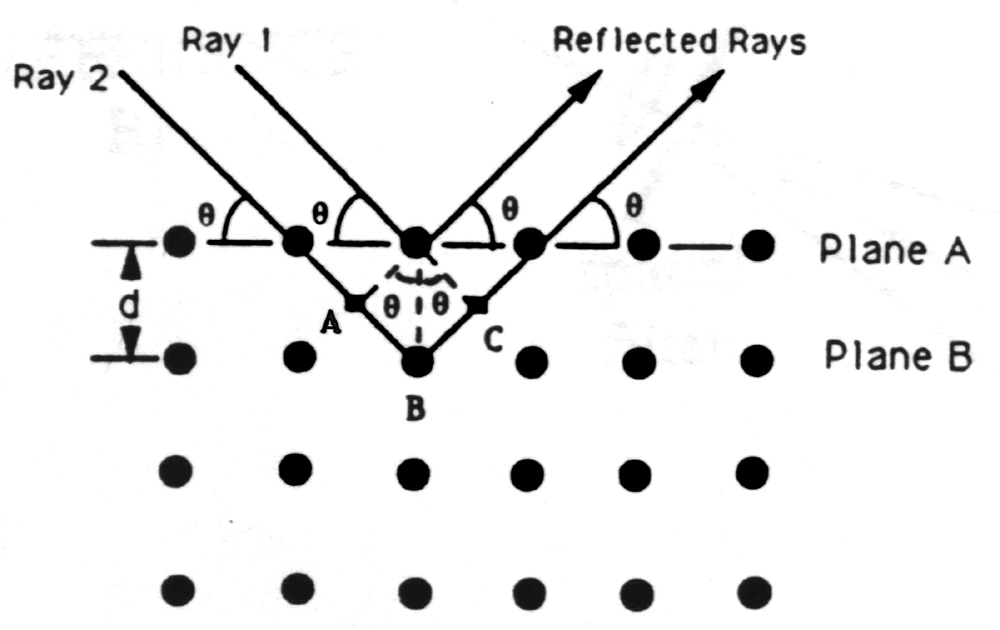
Not long after Röntgen’s 1895 discovery of X-rays, W. L. Bragg used X-rays to study the structure of crystalline solids. In 1912 he proposed a simple model to explain the occurrence of interference maxima in X-rays scattered by a crystal. He pictured the crystal as composed of a stack of parallel planes of atoms, each plane allowing some X-rays to pass but, mirror-like, reflecting some of the X-rays striking it. A beam of parallel X-rays incident at angle J measured from the plane is thus reflected at J from the plane. Reflections from successive planes of spacing d travel paths which differ in length by 2d sinJ; if this path difference consists of a whole number of wavelengths, then the reflected waves interfere constructively. There results the famous Bragg condition for constructive interference:
nl = 2d sinJ, n = integer.

Notice that for X-rays that satisfy the Bragg condition the net deviation from the original direction of travel is 2J.
X-rays with l~ 1 Å = 0.1 nm are ideal for probing crystal structure, because this l is of the order of the interatomic (interplane) spacing. With E = hc/l, this corresponds to an X-ray energy of about10 keV.
There is nothing in Bragg’s model that restricts it to electromagnetic radiation. DeBroglie proposed in 1923 that "particles", such as electrons, have a wavelength given by l = h/mv. For electrons, l ~ 1 Å if p = 10 keV/c or 5 x10-24kg m/s; these are nonrelativistic because pc « mc2 = 0.511 MeV.
If there were only a single set of planes of spacing d, there would be one set of interference maxima; this would be analogous to the fringes observed in the diffraction pattern of a pair of slits or a diffraction grating. (The crystal is really a "grating" with many "lines" separated by ~ 1 Å!) But within the three-dimensional structure of the crystal, many sets of parallel planes can be identified; each gives rise to a set of interference maxima.
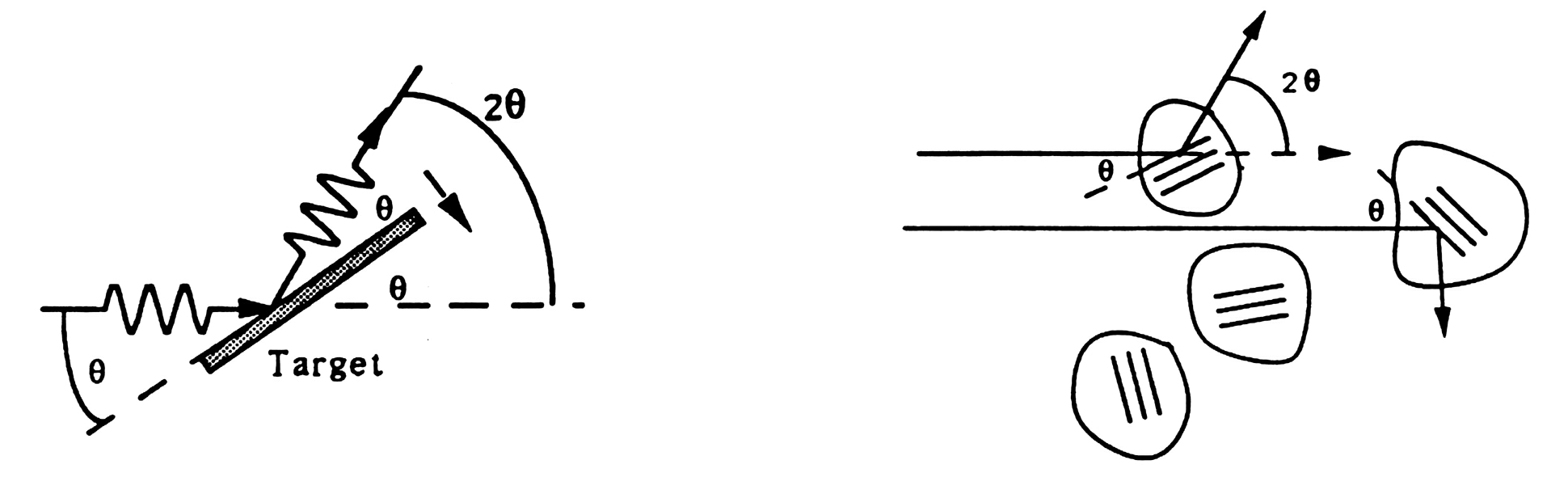
If the sample is made up of many tiny crystals, as is the case for a powder, the Bragg condition for a set of planes with spacing d can be met in any of the tiny crystals which have those planes oriented at J to the incident radiation. If the crystals are randomly oriented, those that meet the Bragg condition scatter radiation into a cone of half-angle 2q about the direction of the incident radiation. In the case of the electron diffraction tube, a ring is visible where the cone of diffracted electron "waves" intersects the phosphor on the inner surface of the tube. In the case of the Scintag X-ray diffractometer, a scintillation detector scans along an arc centered on the sample and in a plane including the incident beam; at the same time, the x-ray generator scans through an angle of q, so that both the generator and the detector are at angles of q to the target. In either case if l is known, from the measured value of 2q and the Bragg condition the interplane spacing d for each set of planes can be obtained.
Interpretation of the Planes
The problem of deducing the crystal structure from the diffraction pattern is in many cases quite difficult. We’ll concentrate on the simplest case, that of a cubic crystal, with just a mention of the hexagonal structure because that is found in the carbon target of the electron diffraction tube.
In solid state physics a crystal is described in terms of a regular, identically repeating array of points called a lattice. The points of the lattice form lines, which need not be perpendicular to each other. Along any one line, each adjacent pair of points is separated by a constant spacing called the latticeconstant in that direction. To obtain the crystal structure, it is necessary to associate with each lattice point an atom or group of atoms, called the basis. Repetition of the basis at each lattice point produces the crystal.
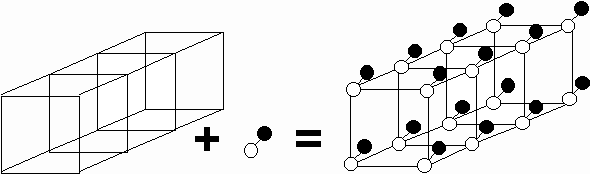
i.e. Lattice + Basis = Crystal
It is somewhat arbitrary how the lattice and basis are chosen to describe a given crystal. It is common to describe a crystal in terms the most conveniently visualized lattice suggested by the symmetry of the crystal.
It is customary to describe crystal planes by a set of Miller indices. To find the Miller indices of a plane
2. Take reciprocals of these numbers and then reduce to the smallest three integers having the same ratio. Enclose in parentheses: (hkl).
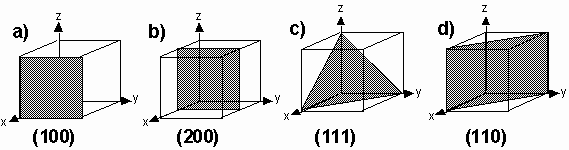
a) intercepts at 1, ¥, ¥ => (100 ) b) intercepts at 1/2, ¥, ¥=> (200)
c) intercepts at 1, 1, 1=> (111) d) intercepts at 1, 1, ¥ => (110)
Note that all planes parallel to each other have the same set of Miller indices. Hence the indices (hkl) may denote a single plane or a set of parallel planes.
It may have occurred to you that the Miller indices specify not lengths but reciprocal lengths associated with the crystal. You know from deBroglie that, aside from a factor of h, reciprocal length is a momentum. The motivation for using the Miller indices to describe a set of planes is that they specify the momentum of the waves scattering from those planes.
There are three fundamental types of cubic lattice.
Simple Cubic (SC) Body-Centered Cubic (BCC) Face-Centered Cubic (FCC)
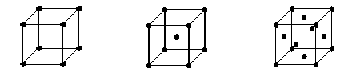
Each lattice is represented here by its conventional (unit) cell; repeating the cell in all directions, like stacking dice tightly together in a box, builds up the lattice. Remember that to obtain the crystal, a basis must be associated with each lattice point.
For a cubic crystal (other forms apply to other crystal structures) the distance (d-spacing) between planes (hkl) is
![]()
Hence the first-order maxima meeting the Bragg condition lie at
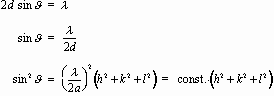
The locations 2J of the peaks in the diffraction spectrum is determined by the d-spacings of the various sets of planes. If the sample is known to consist of only a single cubic material, each set of planes must correspond to some "slice" through the cubic array of atoms. Because hkl are integers, searching for a combination of integers (h2 + k2 + l2) to correspond to every value of sin2J allows determining the constant in the equation above, and hence for known l determines the lattice constant a.
For a simple hexagonal crystal such as graphite, the lattice is as shown below. The (100) and (110) planes, which respectively give rise to the inner and outer rings in the electron diffraction tube, are shown at right; the ratio of the d-spacings d100/d110 = SQRT(3):1.
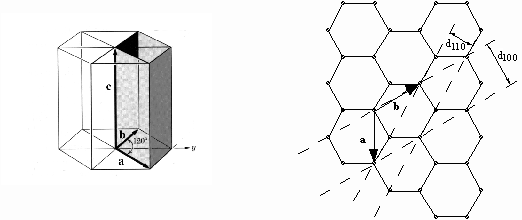
Understanding Intensities of Diffraction Maxima
Bragg’s simple model does not consider the nature or distribution of atoms making up the reflecting planes, and therefore it fails to explain the experimentally observed result that some diffraction maxima are more intense than others. The scattering is actually done by atoms in the crystal. Some atoms may be more effective than others in scattering, particular arrangements of atoms may give rise to anything from strong constructive interference to completely destructive interference.
We are not presently set up to measure quantitatively the relative intensities of electron waves scattered into different directions J, so the following discussion focuses on the relative intensities of scattered X-rays, which are measured with the Scintag XDS 2000.
The effectiveness of an atom for scattering X-rays is due to the number and distribution of electrons in the atom, so we would expect an atom of high Z to scatter X-rays more strongly than an atom of low Z, unless the X-ray wavelength were so short that there could be destructive interference of scattered X-rays within the atom. The scattering effectiveness of each type of atom is taken into account in an atomic form factor f.
If N atoms are in the basis associated with one lattice point, X-rays scattering from these atoms may interfere constructively or destructively depending on the positions of the atoms. The arrangement of the atoms and their individual atomic form factors are included in the structure factor Shkl.
![]()
For example, consider the structure
factor for a monatomic face-centered cubic crystal. The basis consists
of just four identical atoms, at coordinates ![]()
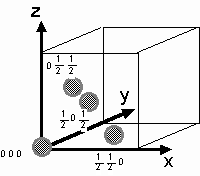
For a monatomic face-centered cubic crystal. Then
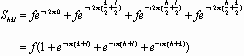
If hkl are unmixed (all odd or all even, counting 0 as even)
Shkl2 = 16 f2
If hkl are mixed
Shkl2 = 0 and there are no reflections.
For example reflections from the (100) planes are missing. Physically this is due to destructive interference from reflection off the (200) planes, which cut through the conventional cell halfway across.

Potassium has atomic number 19, while
chlorine and bromine have atomic numbers 17 and 35, respectively. Because
the C1- and K+
ions have the same number of electrons, their atomic form factors are nearly
equal, and KCl "looks" to the X-rays as if it were a monatomic simple cubic
lattice of lattice constant a/2.
PART 1 - Bragg Diffraction of X-Rays
In one of the two weeks of this experiment, you will use the Scintag XDS 2000 to study X-ray diffraction from powdered crystalline samples. The experimental setup looks something like the figure below. We’ll be using the Ka X-ray of copper, which has l ~ 1.54 Å.

You’ll learn how to prepare a sample for study. In order to get the relative intensities of the diffraction peaks correct, it is important that the powder is deposited randomly on the slide.
For Your Report - Bragg Diffraction of X-Rays
The KCl spectrum differs qualitatively from the KBr spectrum. If you interpret the crystal structures so that both compounds have about the same value of the lattice constant a, only peaks with even indices are present in the KCl spectrum. Explain, for example, how destructive interference eliminates the (111) peak but not the (222) peak in KCl; why is the (111) peak present in KBr?
2. Results of X-ray studies are tabulated in the JCPDS (Joint Committee on Powder Diffraction Standards) Powder Diffraction File. The File is available on microfiche, and there is an annually updated index to the JCPDS file. Use the index to look up the data on KCl and KBr, and compare your results to these. Make a table to compare your results to those on the file.
3. You will also be given an unknown sample to study. Record its X-ray powder diffraction spectrum. You have the d-spacings and Miller indices for each peak from your data. Record relative intensities of peaks from your data.
4. Describe your attempt to identify
the unknown substance from its X-ray diffraction spectrum and record your
best guess. To start the process, use the Search Manual which accompanies
the JCPDS Powder Diffraction File. For a vast number of substances
the Search Manual lists the 8 strongest diffraction peaks, in order
of decreasing intensity. The peaks are identified by the corresponding
d-spacing. To identify an unknown, start by finding an entry in the Search
Manual whose strongest two peaks match the strongest peaks in the X-ray
spectrum of the unknown. [Warning: Due to uncertainty in the values
of the d-spacings, it is necessary to search the entries a little above
and below your values for the d-spacings for these two peaks, as you try
to get the best overall match.] If the other 6 peaks in the Search
Manual entry match the next strongest peaks in the unknown’s spectrum,
the identification is quite likely correct. Confirm the identification
by going to the Powder Diffraction File to check the complete pattern.
[This is harder than it sounds because the 2J
values and d-spacings are determined more reliably than the relative intensities
in this experiment, so even if you correctly locate all peaks in the diffraction
spectrum, you may not be able to identify the unknown substance because
of disagreement with the JCPDS File about the ranking of
peak intensities.] Calculate the lattice constant a for your unknown cubic
substance.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
PART 2 - Bragg Diffraction of Electrons
For the other of the two weeks of this experiment, you will study diffraction of electrons in a tube which somewhat resembles the CRT of a television set. Electrons are boiled off an indirectly heated cathode, then accelerated with a positive high voltage of 2.5 - 5 kV. The electrons pass through a target which consists of graphite, only a few molecular layers thick, vapor-deposited on a micromesh nickel grid. The target is crystalline in tiny regions, so a "powder" diffraction pattern results, seen as a pair of rings around a central spot on the luminescent screen. This is a powerful demonstration of the wave nature of electrons.
*** Click Here for Link to 3D Picture of Graphite Lattice (2 different orientations) ***
WARNING: PROTECT THE DELICATE GRAPHITE TARGET. Do not leave the electron beam on longer than necessary for your measurement. Keep an eye on the target to make sure it is not beginning to glow red hot.

As the accelerating voltage V is increased, the electron’s deBroglie wavelength decreases according to
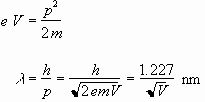 (1)
(1)
In accordance with the Bragg condition nl = 2d sinJ, as the accelerating voltage is increased, the scattering angle gets smaller, and so does the diameter D of the diffraction ring corresponding to a particular d-spacing in the crystalline graphite target.
The figure indicates the geometry. The distance from target to fluorescent screen is given by the tube’s manufacturer as L= 0.140 ± 0.003 m.
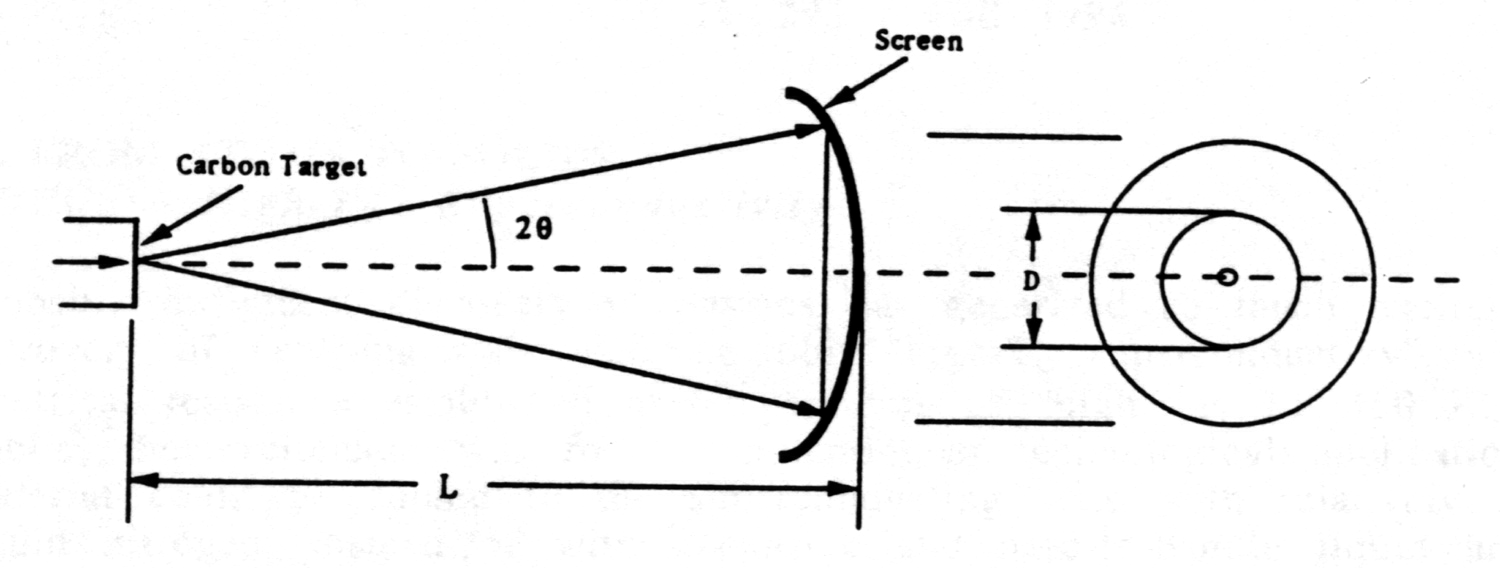
The cone’s half-angle 2J does not exceed about 15o = 0.26 radians, so use of the small-angle approximation is justifiable:
![]()
Then from the Bragg condition for first order n = 1
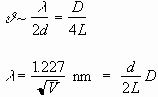 (2)
(2)
Thus the slope of a plot of ![]() can be used to obtain the interplane spacing d.
can be used to obtain the interplane spacing d.
For Your Report - Bragg Diffraction of Electrons
1. Can you demonstrate that it really is electrons and not photons that are being diffracted? Got a magnet? (Don’t try this at home with your color TV!)
2. Plug in the values of fundamental constants to derive the constant 1.227 which appears in equation (1).
3. Measure the diameters of the diffraction
rings at the luminescent screen as a function of accelerating voltage V.
Set-up your own spreadsheet. Estimate error and add error bars. For each
ring make a plot of ![]()
and obtain the slope and its uncertainty.
From the slope obtain the interplane spacings d100
and d110. You should estimate the experimental uncertainty
in each measured quantity in equation (2), and so obtain the estimated
uncertainty in each of your d values.
For Your Report - Thinking about Bragg Diffraction of Electrons and X-Rays
1. What is the main difference between the experimental apparatus in the x-ray diffraction rig and the e-diffraction rig that would account for the fuzziness one observes in the ring in the e-beam data in contrast to the narrowness of the peak in the x-ray data?
| This document was last modifed on Tuesday, 19-Sep-2000 17:57:32 EDT
and has been accessed times. Address
comments or questions to:
|