
where C2 = 3645.6 x 10-8 cm and n = 3, 4, 5Ö. Although only 4 lines were known by Balmer when he started the paper, 10 other lines in the violet and ultra-violet had been measured by the time he finished its writing!
Atomic Structure and Atomic Spectra
Equipment used:
Incandescent lamp, H, He, Hg, Na & K discharge tubes, hand-held spectrometers and diffraction gratings, 1.5 m spectrograph (Rm 1), prism spectrometer (Rm 42), ccd-based optical multichannel analyzer (OMA), PC & spreadsheet.
Objectives:
- visually observe blackbody and atomic spectra
- record the visible-near
UV spectrum of atomic hydrogen using an OMA and relate the observed Balmer
series emission lines to the
predicted energy level diagram of the H atom - develop spectroscopic notation.
- measure the spin-orbit
splitting of sodium and potassium "D-lines and determine the sizes of the
magnetic fields experienced by the
"optical electrons" in the upper levels for those those transitions.
References:
R. Harris, Nonclassical Physics: Beyond Newton's View, Addison Wesley, Menlo Park, California (1998).
R. Serway, C. Moses, and C. Moyer, Modern Physics, Second Edition, Saunders College Publishing, Fort Worth, Texas (1997).
K. Krane, Modern Physics, Second Edition, John Wiley & Sons,
New York (1996).
Spectra - a brief history
Blackbody, atomic and molecular spectra (intensity as a function of wavelength or frequency) have been the subjects of intensive examination for nearly 200 years (Fraunhoferís observations of dark lines in the solar spectrum, including the "D" lines, were made in 1814!). For nearly half that time, the study of the optical spectra associated with heated solids and atoms and molecules in the gas (or plasma) phase was of essentially an empirical nature.
For the continuous blackbody spectra, the empirical relations developed by Wein (Weinís displacement law) and by Stefan and Boltzmann during the latter part of the nineteenth century lacked a theoretical foundation. On a Sunday evening in early October of 1900, Max Planck discovered the blackbody formula that allowed an exact prediction of the shapes of blackbody spectra. Planckís formula allowed the derivation of Weinís law and the Stephan-Boltzmann law, and provided the source of the empirical constants contained within them. To derive his formula Planck had to assume that electromagnetic radiation was quantized. Quantum physics and the photon had been invented!
A similar situation obtained with respect to the discrete line spectra of atoms and the associated band spectra of molecules. Accurate measurements of the four visible emission lines of atomic hydrogen had been made by Angstrom (who labeled them alpha, beta, gamma and delta). In 1885 Balmer published a paper entitled "Notice Concerning the Spectral Lines of Hydrogen," which included an empirical formula for the wavelengths of the lines measured by Angstrom. Balmer's formula was

where C2 = 3645.6 x 10-8 cm and n = 3, 4, 5Ö.
Although only 4 lines were known by Balmer when he started the paper, 10
other lines in the violet and ultra-violet had been measured by the time
he finished its writing!
It 1913, Niels Bohr announced the first theoretical explanation of the spectrum of the hydrogen atom (although his basic ideas are applicable to other atomic systems as well). Bohr assumed that the angular momentum of the electron in its "orbital" motion about the proton was quantized (which had the effect of quantizing the electron's orbital radius and energy). He further assumed that when an electron undergoes a transition from one allowed orbital state to another, it can do so by emitting or absorbing radiation whose energy equaled the energy difference between the orbital states involved. According to Bohr, the allowed energies of an electron bound to the proton in a hydrogen atom were given by,
![]()
where n = 1, 2, 3Ö. Thus, Balmer's empirical formula gained a theoretical
foundation. Note that Bohr's theory requires only a single quantum number
(the principal quantum number) to explain the observed spectrum.
The Modern View
Bohrís theory included an explanation for the lack of radiation that classical electromagnetic theory predicted should arise from orbiting electrons: the electrons were in "stationary states." In other words he said they didnít radiate when they occupied an allowed orbit, never mind that they were undergoing centripetal acceleration due to their orbital motion! Needless to say, the argument was less than convincing to many.
In an effort (successful!!) to explain Bohrís angular momentum assumption, DeBroglie (1923) interpreted Bohrís postulate in terms of wave resonance. The result was the DeBroglie relation,
![]()
Three years later, Schrodinger introduced his wave equation, whose solutions are the wavefunctions for a particle trapped in a potential well. Since the wave function contains all that is knowable about a particle that is behaving as a wave, when Schrodinger's equation is applied to an electron bound to a single proton (the hydrogen atom), Bohr's formula for the allowed energy levels for the electron must necessarily be contained in the resulting solutions.
The solution of Schrodinger's equation for the problem of the H-atom is far too involved to reproduce here (see references). Indeed Bohr's relation for the electronic energy levels in the hydrogen atom is a result of that solution. However, such a full quantum mechanical treatment also results in two other quantum numbers in addition to Bohr's principal quantum number n. That is, the energy for a hydrogen atom electron is determined by the principal quantum number, but for each n, there are also other quantum numbers required to fully describe the allowed energy levels of the H atom. Those quantum numbers are the electronic orbital-angular-momentum quantum number l, and the magnetic quantum number m (which quantizes the z-component of the electron's orbital angular momentum). Further results of the Schrodinger equation for the hydrogen atom place restrictions on the allowed values of m and l. Those restrictions are:
- For each value of the principal
quantum number n, the possible values for the angular momentum quantum
number l are l =
0,1,2Ö..(n-1).
- For each value of l, there are 2l + 1 possible values of m ranging from -l to +l (in integer steps of course, and including zero)
That set of restrictions together implies n2 different wavefunctions that describe n2 different possible states for the electron for each principal quantum number n. This seriously complicates the energy level diagram for the electronic states of the hydrogen atom over the rather simple case suggested by Bohr's work.
Although it is not a result of any solution to Schrodinger's equation, it is nevertheless a fact that electrons possess an intrinsic spin that is also quantized. The allowed values of the electron spin quantum number s are + 1/2 and - 1/2 (or spin up, and spin down). Thus, the number of possible unique wave functions for each principal quantum number n described in the previous paragraph must be multiplied by 2!
The net result is that 4 quantum numbers (n, l, m & s) are required
to fully specify any given allowed state of an electron bound to a hydrogen
atom. When this fact is coupled with the Pauli exclusion principle (no
two electrons bound to an atom can possess an identical set of quantum
numbers) and generalized to other atoms, the periodic table of the elements
is explained!!!!!!
Spectroscopic Notation and Transition Selection Rules
A shorthand notation for the possible electronic energy levels in an atom involves specifying the principal quantum number of the electron, the total electronic angular momentum due to spin, and the total electronic orbital angular momentum, and the total electronic angular momentum i.e. n, L = l1 + l2 + l3 Ö, S = s1 + s2 + s3Ö, and J = L + S (yes, they are vectors!). The notation is known as L-S coupling notation since the total electronic angular momentum is simply the vector sum of the electronic orbital and spin angular momenta. The notation is written as,
n 2S + 1LJ,
where 2S + 1 is known as the multiplicity of the state (the terminology
is 1 = singlet, 2 = doublet, 3 = triplet, and so on). For historical reasons,
L = 0 is referred to as an S-state, L = 1 is a P-state, L = 2 is a D-state,
L =3 is an F-state and the alphabet is followed thereafter. As an example
of an application of this notation, the ground state of the hydrogen atom
is 12S1/2.
Since a photon carries energy and angular momentum (1 unit), any electronic transition from one allowed energy level to another must conserve energy and angular momentum for the atom-photon system. Thus, restrictions on the allowed changes in multiplicity, orbital and total angular momentum can be partially understood. These restrictions are known as selection rules and they are,
![]()
with J = 0 to J = 0 forbidden. Any allowed transition between two electronic
states must obey these selection rules.
Notice that the magnetic quantum number does not appear in the spectroscopic notation. The reason for this is that effects on electronic energies in atoms due to quantum number m are only realized if the atom is placed in an external magnetic field (Zeeman effect). Nevertheless, the selection rule still applies and is written,
![]()
Spin-Orbit Interaction
Given that an electron spins and that it is charged, it should come as no surprise that it possesses a magnetic dipole moment (i.e. it is a tiny compass needle). Also given that an electron bound to an atom is in some sense in motion relative to the nucleus and any other bound electrons, it experiences a magnetic field due to that motion. Given further that an electron's spin is quantized (it can take on only 2 values), the interaction between the electron's magnetic moment and the magnetic field it experiences due to it's orbital motion should result in an energy difference between otherwise similar electronic levels if the electron's spin is aligned parallel or anti-parallel to the magnetic field. It turns out that the energy difference between spin-up and spin-down states is just
![]()
Where B is the magnetic field due to the orbital motion and mu is the
Bohr magneton (i.e. the electron's magnetic moment). By measuring energy
differences between spin-orbit split levels in atoms, the magnetic field
experienced by the electron due to its orbital motion about the nucleus
can be easily determined. This effect is not easily observable in the spectrum
of the hydrogen atom, but is easily observed in the spectra of sodium and
potassium atoms. Measurements of the visible-near UV spectrum of the hydrogen
atom (Balmer series), and portions of the spectra of Na & K atoms (the
"D" lines) atoms are the experimental goals of this lab.
Pre-lab questions.
How would you justify the layout of the first three rows of the periodic table based upon the information supplied above?
Determine the spectroscopic notation for the ground states of H, He, Li, Be, Na, K, Rb and Cs.
Construct a complete energy level diagram for the H atom based upon Bohr's explanation of the H atom only.
Construct
an energy level diagram up through n = 3 for the H atom, based upon the
results of application of Schrodinger's equation to
the problem of the H atom. Determine all possible transitions between allowed
levels in the H atom that give rise to H-alpha radiation.
The Experiment
Three spectroscopic measurement tools (spectrometers) will be employed to accomplish the goals of this laboratory exercise. Two are antiques that have the wonderful advantage of allowing you to actually see the spectra of interest with your own eyes. In addition, some hand-held spectroscopic instruments which can be used to observe the spectra of various light sources will be available for use. The key quantitative spectroscopic measurement tool available is a ccd-based optical multichannel analyzer that will allow quantitative measurements of the spectra of interest (H, Na & K). Spectra will be recorded onto floppy disks in a format that can easily be imported into a spreadsheet for analysis and production of plots of the spectra.
1) H-atom (Balmer series)

Where l and u refer to lower- and upper-level principal quantum numbers, respectively, Z is the atomic number (here Z=1) and R = 1.097373 x 107 m-1 is the Rydberg constant.
We will measure the Balmer series of spectral lines from a hydrogen discharge tube, determine the wavelengths of the Balmer lines experimentally, and, using the above formula, experimentally determine the value of the Rydberg constant. It is left to the student to determine how this should be done, given the wavelenghts of the Balmer lines (and the attendant uncertainties in wavlenght) derived from the recorded spectra, and the Rydberg-Ritz formula shown above.
Bohr's model for the H atom predicts the value of the Rydberg constant.
It is an interesting combination of fundamental constants (find it in your
favorite physics text!!!). Calculate Bohr's prediction for the Rydberg
constant and compare it to your experimentally derived value. You should
also use your experimentally derived value for the Rydberg constant to
determine the value of the ionization potential of the H atom. That too
is an interesting combination of fundamental constants (find it too in
your favorite physics text). Compare your measured value to the prediction
of Bohr.
2) Spin-orbit interaction (magnetic fields in atoms, Na & K "D" lines), spectroscopic notation, and selection rules.
A brief discussion of the spin-orbit interaction in atoms, spectroscopic notation and the selection rules for allowed (dipole) transitions between stationary states in an atom is found above. We will measure the spectra of Na and K in the vicinity of their respective "D" lines. The "D" lines in alkali atoms are transtions from the first excited states (spin-orbit-split states) to the ground state. As noted above, the splitting is due to the interaction between the magnetic dipole moment of the electron (due to its intrinsic spin, a constant), and the magnetic field it experiences due to its "orbital motion" relative to the nucleus (and inner electrons). From the observed spectra, you are asked to determine the spin-orbit splitting (an energy), and, using the known magnetic moment of the electron, determine the size of the magnetic field (in Tesla) experienced by an electron in the first excited states of Na and K. You should compare those fields with the sizes of magnetic fields that can be produced by research laboratory magnets. (The point here is that they are charged particles that are subject to the normal interactions expected from the results of electromagnetic theory.)
Based upon the magnetic field values you find, predict how the magnetic fields experienced by an electron in the first excited states of Rb and Cs would compare to those measured for Na and K. Also, predict, based upon extropolations from Bohr's model, how the magnetic field experiened by electrons in higher excited states (spin-orbit, but larger orbits!!!) of an alkali atom would vary with increasing principal quantum number. (There's a lot more that's periodic about the periodic table than boiling points and melting points!!!!) Determine the spectroscopic notations of the the upper and lower levels of the transitions that give rise to the "D" lines in Na and K. Verify that the selection rules described above are followed for those transtions (note: you cannot verify the selection rules on the magnetic quantum number m from your data??? Why not??) Finally, based upon the selection rules, predict the transitions that you would expect between allowed D- and P-states in an alkali atom (any alkali atom, chemical symbol Ak (hehehehe)).2) Abbreviated theory of CCD-image chip operation.
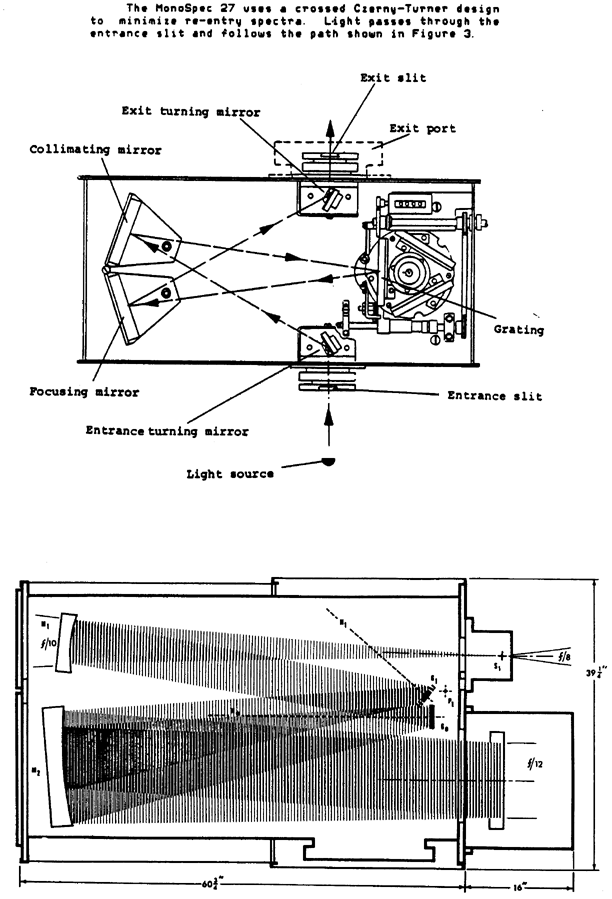
Appendices: 1) spectrometers used here (upper: 0.27-m Jarrel-Ash Spectrograph - CCD, lower: 1.5-m Jarrel-Ash
spectrograph)
| This document last modified on Sunday, 01-Oct-2000 20:22:28 EDT
and has been accessed [an error occurred while processing this directive] times.
Comments and suggestions should be addressed to:
|