Equipment used:

64 cc intrinsic germanium detector, scintillation spectrometer with NaI(Tl) crystal, multichannel analyzer card in personal computer

Objectives:

1. to record gamma ray line spectra and to interpret them in terms of transitions between nuclear states
2. to consider how the strong nuclear interaction between nucleons gives rise to the properties of nuclear states: simple models of the interaction and its consequences may rather successfully describe low-energy nuclear states

Nuclear Shell Model

Every atomic nucleus except the simplest form of hydrogen contains two or more nucleons - protons and neutrons - which interact via the strong nuclear force. Study of this interaction shows that it cannot be described by a simple expression such as that of the Coulomb law for the electrostatic force. A successful approach represents the interaction between nucleons with a potential, which depends on the orbital and spin angular momentum of the nucleons, as well as the - perhaps fluctuating - shape of the nucleus as a whole. The simplest representation is the single-particle shell model, which uses an average potential well to represent the interaction of one nucleon with all other nucleons of the same type. (There are separate wells for protons and neutrons.)

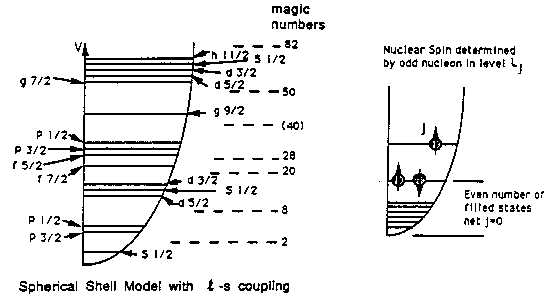
One of the features of the periodic chart of the nuclei which must be explained by the shell model is the occurrence of so-called "magic numbers" of nucleons. Just as atoms with certain numbers of electrons are particularly stable (noble gases), there exist particularly stable nuclei with certain "magic" numbers of protons or neutrons. If one of these magic numbers is n, then the (n + 1)^th nucleon is much less tightly bound than the n^th. In the shell model, this means that the (n + 1)^th nucleon is bound in a state which is not so deep in the potential well as is the state of the n^th nucleon. The magic numbers have been found experimentally to be 2, 8, 20, (28), (40), 50, 82, 126 ... protons or neutrons, where the "magicity" is less pronounced at 28 and 40.

Two simple guesses at the shape of this attractive well quickly suggest themselves: the infinitely deep spherically symmetric square well, and the three-dimensional isotropic harmonic oscillator. Within these wells, only certain discrete energy states are allowed, the result of boundary conditions on the nucleon wave function and its slope at the edge of the well. The Pauli principle tells us how many nucleons can fit into each of these states. The magic numbers predicted by these models are those numbers of nucleons which just fill each state (plus all other states of lower energy) in turn. However, these predicted magic numbers do not jibe with the experimentally determined magic numbers, so these models have to be rejected.

But another guess proved to be successful. Following a suggestion by Enrico Fermi, Maria Goeppert Mayer in 1949 figured out a nuclear shell model which includes coupling between the orbital angular momentum l and the intrinsic spin s of the single nucleon moving in the average nuclear potential. In this model the potential well is spherically symmetric and is intermediate between the infinite spherical square well and the three-dimensional isotropic harmonic oscillator. This shell model was so successful in predicting magic numbers, spins and parities of nuclei, as well as other nuclear properties, that Mayer received the 1963 Nobel Prize for her work.

The accompanying sketch shows the levels in this model. The subscript on the level designation indicates the value of

j = l + s, i.e. j = l ± 1/2.

Assume that in the state of minimum energy an even number of nucleons couple their j vectors antiparallel in pairs to give a net j of zero. With this assumption we conclude that the ground state of every nucleus with both an even number of neutrons and an even number of protons ("even-even" nucleus) has a total j = 0. This is confirmed by experiment. This assumption also leads to the conclusion that the total ground state j and parity of a nucleus with an odd number of nucleons ("odd" nucleus) is determined solely by the state of the least tightly bound nucleon. For example the j and parity of a nucleus with an odd number of protons and an even number of neutrons equal the j and parity of the last proton.

With this single-particle shell model we immediately predict (correctly!) that ¹³⁷Cs₅₅ has a ground state spin and parity of  7/2⁺, since there is an even number of neutrons and the least tightly bound proton is in a g_7/2 state. And after experiments teach us that the higher-energy states do not necessarily fill in quite the order expected from the picture on the preceding page, it seems plausible that the ground state of ¹³⁷Ba₈₁, should be 3/2⁺ (d_3/2 neutron) . Furthermore, if one considers that in some cases nuclear excited states are attained by supplying the energy E to lift "outer" nucleon from its lowest available energy level to a higher level, one can understand some nuclear excited states in terms of this same shell model.

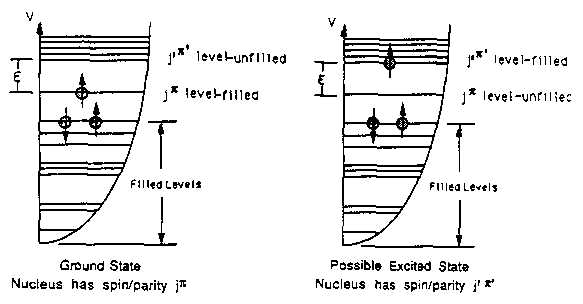
In particular, we may interpret the 11/2^- excited state of ¹³⁷Ba at 662 keV as arising because there is an unpaired neutron in an h_11/2 state; this state turns out to be 662 keV above the d_3/2 ground state.

The nuclear shell model which has just been described gives its most successful predictions for properties of nuclei which are nearly spherical; its predictions are wrong for nuclei which are distorted in shape. This comes as no surprise, for a spherically symmetric potential well (and hence a spherically symmetric distribution of nucleons represented by the well) was assumed as part of the model. Experiments sensitive to nuclear shape reveal that the nearly spherical nuclei are those which have proton number Z and/or neutron number N near to a magic number. It seems plausible then that the spherical shell model satisfactorily predicts properties of nuclei such as ³H (Z=1, N=2), ¹⁷0 (Z=8, N=9) , ⁴¹Ca (Z=20, N=21), and ²⁰⁷Bi (Z=83, N=124), but not for ¹⁶⁷Er (Z=68, N=99). More general shell models, which relax the requirement of spherical symmetry, have been introduced to describe nuclei which have deformed shapes, which can even be fluctuating.
 

Part I – Single-Particle States Of An Odd-A Nucleus

Sinqle-Particle Lifetimes

Lifetimes have been computed for nuclear excited states modeled simply as an inert core of A-1 nucleons, plus a single nucleon in a spherical shell model state (Blatt and Weisskopf, Moszkowski). Consider a transition between two shell model states of this nucleon: an excite state j_i^pi with energy E_i decays to a state j_f^pf with energy E_f, with emission of radiation of energy E = E_i - E_f.

Isomeric States

An excited state with a "measurably long" half life (this is often arbitrarily interpreted to mean longer than 0.1 sec) is called a metastable or isomeric state.

Nuclear isomeric states are not found uniformly among all nuclei but are preferentially concentrated in "islands of isomerism" -- nuclei with Z or N just below magic numbers. We can understand the "islands of isomerism" in terms of the shell model. As the nucleon shell approaches closure at a magic number, for states fairly high up in the potential well (see the figure on page 2) shell model states of very different spin J can occur close together in energy. If the least tightly bound nucleon is to make a transition between two such states there must be a large ?j with small E -- just the condition for long lifetime of an excited state! So the decay is slow and the excited state is an isomeric state. Typical isomeric transitions are g_9/2 à p_1/2, h_ll/2 àd_3/2, etc.
 

FOR YOUR REPORT - SINGLE-PARTICLE STATES OF AN ODD-A NUCLEUS

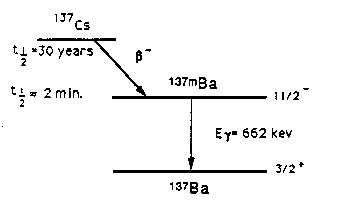
1) First we consider the decay of the isomeric state ^137mBa as an illustration of a single-particle transition in a nearly spherical odd-A nucleus. ^137mBa has a half life of about 2 minutes. It is produced by the decay of ¹³⁷CS, which has a half life of 30 years. Actually the familiar 662-keV gamma ray is emitted in the decay of the daughter ^137mBa, not directly by the parent ¹³⁷Cs. Relevant parts of the decay scheme are shown in the figure below.

For our experiment we use the Multichannel Scaling mode of the multichannel analyzer card. The amplified voltage signal corresponding to detection of the 662 keV gamma ray is passed through a single channel analyzer, which gives a 5-volt ½-ms logic pulse whenever a gamma ray is detected. The multichannel analyzer is preset to count in one channel the number of these pulses detected in 4 seconds; then it records in successive channels the number of counts in successive 4-second intervals. The process is repeated for background subtraction. From the decaying number of counts per channel, the half life of ^137mBa is readily obtained.

You've already become accustomed to the PCA-II software, and there are only a few new points to learn.

In your spreadsheet you can take the logarithm of the counts per channel and determine the half life by fitting a straight line to the relation

You should use the spreadsheet to graph your data and your fit.

2) The 662-keV transition carries away 4 units of angular momentum and results in a change in parity of the nuclear state of ¹³⁷Ba. For a single particle transition which does this, theoretical calculations of the half life have been performed. The results for t_1/2 in seconds are

(Weisskopf) t_1/2 = ln2 [3.3 x 10^-6 A² E_g⁹]^-1

(Moszkowski) t_1/2 = ln2 [4.8 x 10^-5 A² E_g ⁹]^-1

Multichannel Scaling with the PCA-II Card

Previously we used the PCA-II card in the PHA (Pulse Height Analysis) mode, where the number of counts in each channel of the memory represents the number of pulses detected with the corresponding photon energy. In the PHA mode, all channels are available simultaneously, and incoming pulses are sorted into the proper channel according to their voltage.

Now we introduce the MCS (Multichannel Scaling) mode, where pulses of a single preselected voltage are recorded in one channel at a time. Counts are stored in channel 1 for a user-selected time interval T, then in channel 2 for the following time interval T, then in higher channels in succession, each for an equal time interval T. The MCS mode is ideal for following the decay of a radioactive source, when the preselected voltage corresponds to the energy of a gamma ray emitted by the source.

I. Starting PCA Software (Note:  If the software is already loaded, skip this step)

    A. At the C-prompt type cd\pca and enter, then type pca 'I' and enter.

II. Setting up to record an MCS spectrum

    Use the mouse to choose from the menu bar.

    A. Setup as usual. One Quarter of the memory is enough. Choose Expanded Display..; 64.
    B. Mode
        1. MCS…
            A. Passes. Choose 1.
            B. Dwell. Choose 4 sec. This is the length of time the analyzer counts in each channel in turn
.
III. Recording a spectrum

    A. Use [F1] and [F2] in the usual manner.
    B. No calibration is done, because the horizontal axis represents time, not energy. The preselected voltage is chosen by external electronics (a single channel analyzer).

IV. Saving a spectrum for spreadsheet processing

    A. File
        1. Ascii File save (Note:  save to a floppy please)

A. Filename. Choose MCSBa137.PRN for the spectrum with the source present, and MCSBKG.PRN for the background spectrum. The software does not provide for changing to subtraction in the MCS mode, so you need to subtract background using the spreadsheet.

    A. Quit. Choose Exit to DOS; (Y).

VI. Spreadsheet  Open the two files you saved the floppy.  (Note:  they are comma delimited files)
    A. Subtract the MCS background from the MCS data file, and obtain the half life of ^137mBa by performing a linear regression fit.
        With the data N (t) = N_oe^-(t/t) you have ln (N/N₀) = -(1/t) t, which is linear; t_1/2 = 0.693 t.
 

Part 2 - Collective States Of Even - Even Nuclei

Collective States

The preceding discussion has focused on a single nucleon, with the remaining nucleons serving only to provide an average potential. This approach is particularly valuable for nearly spherical odd-A nuclei. In other cases, however, it is most helpful to consider not individual nucleon orbits but collective motion of the nucleus as a whole. (Of course, the nucleus is still made up of the nucleons, whose motions define the motions of the whole nucleus.) Simple models of this type can be applied with some success for even-even nuclei which are nearly spherical and vibrate like a liquid drop, and for even-even nuclei which are ellipsoidal and both rotate and vibrate.
 

Vibrations of Nearly Spherical Even-Even Nuclei

For the three-dimensional harmonic oscillator, energy of excitation is quantized so that excited states are equally spaced in energy. A nucleus can undergo quantized shape vibrations; the quantum of vibrational energy is called a phonon. Even if the vibration is symmetrical, it can contain angular momentum if the shape distortion travels around the nucleus as a wave.

Consider vibrational excitation of a nearly spherical even-even nucleus. The ground state is necessarily 0⁺. Ordinarily the lowest-energy excited state is 2⁺, so the phonon in this case carries 2 units of angular momentum. The nucleus oscilates between prolate ("football") and oblate ("pumpkin") axially symmetric shapes; these have a quadrupole moment, and so this is referred to as a quadrupole vibration. A two-phonon state is expected to have twice the energy of the one-phonon state (measured from the ground state). The angular momentum of a two-phonon state is obtained by vectorially adding the angular momenta of two spin-2 phonons: the result may be 0, 2, or 4 (1 and 3 are ruled out because the integer-spin phonon is a boson.) If there is slight anharmonicity inthe vibration, these three two-phonon states may have slightly different energies and be resolved as a so-called "vibrational triplet" of states: 0⁺, 2⁺, 4⁺. According to this simple model, the occurrence of a "vibrational triplet" at about twice the energy of the 2+ first excited state is taken as evidence that the oven-even nucelus is nearly spherical and undergoing vibrational excitation. There actually are cases known where near-spherical even-even nuclei possess 0⁺, 2⁺, and 4⁺ states at about twice the energy of the 2⁺ first excited state, and for these nuclei the simple vibrational model seems to have some validity. But it should not be taken too seriously; many other near-spherical even-even nuclei have not been found to have all three members of the triplet, or they have "extra" states at about twice the energy of the first 2⁺ state.

Another possible collective excitation is the octupole vibration. In this mode the nucleus undergoes pear-shaped distortions, with the "stem end" and the "blossom end" exchanging places periodically. The phonon in this case has angular momentum and parity of 3^-. Experimentally the lowest octupole vibrational state is found at higher energy than the lowest quadrupole vibrational state; the nucleus is "stiffer" against octupole vibrations.
 

Collective Excitations of Ellipsoidal Nuclei

When a nucleus is distorted so that it has a permanent axis of symmetry, then it's possible for that axis to precess, and we can recognize rotation of the nucleus. Classically, for a rotating object with angular momentum J and constant moment of inertia I, the rotational energy is E(J) = (1/2I) J² .  Quantum mechanically J² is replaced by an operator whose eigenvalues are J(J+1)h².

For a symmetrical nucleus (one whose appearance is unchanged when you look at it in a mirror) the allowed states have even parity: (-1)^J = +1. Therefore only even values of J are allowed: J = 0, 2, 4, 6, ... and the energies of the rotational states are in the ratio

E_O: E₂: E₄: E₆: ... = 0: 6: 20: 42:

so the excited states have energies in the ratio

1: 3.3: 7: … .

Occurrence of states 0+, 2+, 4+, 6+, ... with excited state energies in the ratio 1: 3.3: 7: … is taken as evidence that an even-even nucleus has ellipsoidal shape and undergoes rotational excitations. For high-spin states the ratio of energies differs from this simple progression in a way that can be understood by assuming that the moment of inertia is not constant: the nucleus stretches as it rotates.

Experimentally, for ellipsoidal even-even nuclei rotation involves less energy than vibration, so the 2⁺ rotational state is the first excited state. However, the nucleus may also vibrate while it rotates. This leads to rotational bands. The lowest-energy state of a rotational band contains the energy of one quantum of vibration; higher states in the band have additional energy associated with the rotational motion. We mention two types of vibration:

• b vibration - a quadrupole vibration, such as would be obtained by pushing and pulling on the pointed ends of a football. The rotational band built on vibration has states 0⁺, 2⁺, 4⁺, …

• g vibration - a vibration losing cylindrical symmetry, such as would be obtained by pushing and pulling on the sides of a football. The rotational band built on g vibration has states 2⁺, 3₊, 4⁺, ... .

Unified Model

All the considerations we've discussed can be pulled together in a unified model of nuclear states: very difficult calculations give the properties of orbits of individual nucleons moving in a nonspherical, rotating, vibrating potential well. Self-consistency is required: the nucleons in the distorted orbits have to give rise to the distorted potential! For their pioneering work on a unified model, Aage Bohr and Ben Mottelson shared in the 1975 Nobel Prize.
 

For Your Report - Collective States Of Even-Even Nuclei

For the remainder of this experiment we consider transitions between states of even-even nuclei, and we attempt to interpret these states in terms of vibrational and rotational excitations.

Because many of the gamma rays emitted in these transitions have nearly equal energies, a NaI(Tl) spectrometer does not have good enough energy resolution to identify them. Therefore we consider spectra obtained with a high-purity germanium detector, which gives lines having FWHM of only a couple of keV. Briefly, the germanium detector is a sort of "solid state proportional counter", in which the incoming photons produce hole-electron pairs; the number of pairs produced is proportional to the energy of the incoming gamma ray, and the charge collected is converted to a voltage signal analyzed in the usual way.

3) First we need to calibrate the germanium spectrometer. You are provided with spectra of the same ²⁰⁷Bi and ²²Na sources you previously used. Again you can use the 75 keV lead x-ray and the 1275 keV gamma ray for calibration. Note the extreme linearity of the spectrometer; with just two points used for calibration, throughout the spectrum you are able to read gamma ray energies to a fraction of a keV.

• You can now resolve the K_al, K_a2, K_b1, and K_b1 X-rays of Pb. Go back to your table of binding energies for Pb, compute energy differences, and identify each of the Pb x rays in the spectrum of ²⁰⁷Bi.
• Determine the FWHM of the 511-keV annihilation radiation peak in the ²²Na spectrum, and compare it to the FWHM of the 570-keV peak in the ²⁰⁷Bi spectrum. What you observe is Doppler broadening of the annihilation radiation: the electrons and positrons don't actually meet at rest, and their distribution of kinetic energy results in a distribution of energy carried away by the photons when they annihilate.

With Z=46 and N=60, ¹⁰⁶Pd is a near-spherical even-even nucleus. At about twice the energy of the 2⁺ first excited state, there are 0⁺, 2⁺, and 4⁺ states which have been interpreted as a "vibrational triplet". A partial decay scheme is shown in the figure.

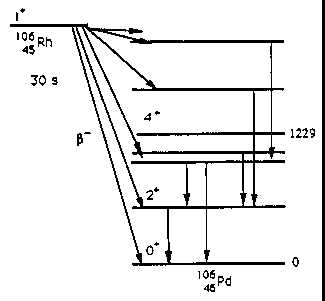
You are required to do two things:

• Find the energies of the first excited state and of the 0⁺ and 2⁺ members of the vibrational triplet in ¹⁰⁶Pd. Are the energies of the three vibrational triplet states equal to about twice the energy of the first excited state?
• Clearly identify which of the vibrational triplet states is the 0⁺ state, and which is the 2⁺ state. Explain how you made the identification. (To answer this you have to recognize that it is not possible for a photon to be emitted in a transition between a 0⁺ state and another 0⁺ state; the photon has an intrinsic spin of 1, and so angular momentum conservation would be violated by such a transition. Therefore if you observe a photon transition between an excited state and the ground state of an even-even nucleus, the excited state cannot be a spin=0 state.)

5) Finally, consider spectra emitted in the decay of 13-year ¹⁵²Eu to ¹⁵²Sm (Z=62 and N=90) and to ¹⁵²Gd (Z=64 and N=88). The daughter nuclei are just at the edge of the transition between nearly spherical and ellipsoidal shape. In the Sm and Gd isotopes the transition takes place suddenly; the addition of just two neutrons is enough to change which shape has lower energy and so is preferred by the nucleus.

You are provided with spectra taken with the source at 10 cm and in contact with the detector, the latter again taken to look for summing. A very large number of gamma rays are emitted, and you are asked to consider only the most prominent transitions, which occur between low-energy states of the daughter nuclei. Confidently disentangling the complex spectrum requires more information than we are equipped to consider in this introductory laboratory, so the spectra you're given have prominent peaks shaded with distinctive colors, according to whether they correspond to transitions between levels of ¹⁵²Sm or of ¹⁵²Gd. In the following decay scheme you are given much of the information known about these low-energy states.

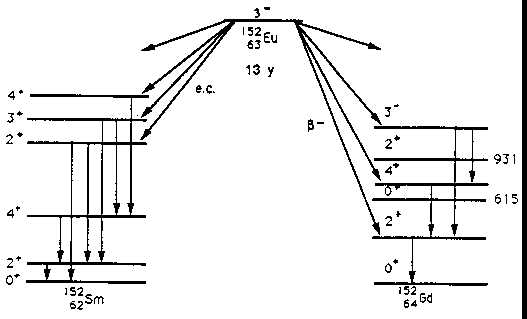
You are required to do two things:

• Determine the energies of the illustrated excited states of ¹⁵²Sm and ¹⁵²Gd populated in the decay of ¹⁵²Eu.
• In each case find the ratios of the energies of low-energy excited states to the energy of the first excited state; use these ratios to identify tentatively each of ¹⁵²Sm and ¹⁵²Gd as either nearly spherical or ellipsoidal.